Vectors
Vectors are 1-dimentional Arrays
Vectors have a Magnitude and a Direction
Vectors typically describes Motion or Force
Vector Notation
Vectors can be written in many ways. The most common are:
| v = |
|
or:
| v = |
|
Vectors in Geometry
 |
The image to the left is a Vector. The Length shows the Magnitude. The Arrow shows the Direction. |
Motion
Vectors are the building blocks of Motion
In geometry, a vector can describe a movement from one point to another.
The vector [3, 2] says go 3 right and 2 up.
Vector Addition
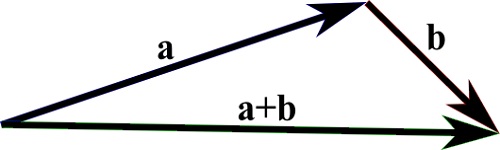
The sum of two vectors (a+b) is found by moving the vector b until the tail meets the head of vector a. (This does not change vector b).
Then, the line from the tail of a to the head of b is the vector a+b:
Vector Subtraction
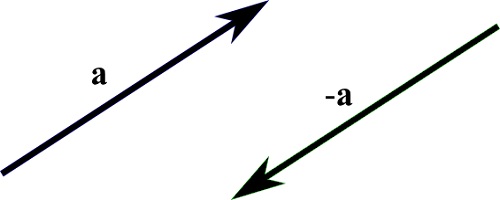
Vector -a is the opposite of +a.
This means that vector a and vector -a has the same magnitude in opposite directions:
Scalar Operations
Vectors can be modified by adding, subtracting, or multiplying a scalar (number) from all the vector values:
a = [1 1 1]
a + 1 = [2 2 2]
[1 2 3] + 1 = [2 3 4]
Vector multiplications has much of the same properties as normal multiplication:
[2 2 2] * 3 = [6 6 6]
[6 6 6] / 3 = [2 2 2]
Force
Force is a Vector.
Force is a vector with a Magnitude and a Direction.
Velocity
Velocity is a Vector.
Velocity is a vector with a Magnitude and a Direction.